Процедурная генерация графов
Мне нужно сделать процедурную генерацию графов. То есть есть функция, которой на вход подаётся номер графа, а на выходе получается список координат точек и список дорог, их соединяющих (точнее процедура будет вызывать по мере необходимости две подпрограммы - add_point и add_way, первая из которых принимает две координаты, а вторая номера точек). Чем больше номер графа, тем больше в нём будет точек и рёбер (ну эту зависимость не сложно придумать, тут я могу сам справиться). При этом пересечений должно быть поменьше, а циклов побольше. Как такое можно сделать?
Могу посоветовать литературу:
-----------------------------------------------------------------
Судоплатов С.В. Элементы дискретной математики. 2002
Элементы теории графов стр. 108
Маршруты. Достижимость. Связность стр. 119
Обходы графов стр. 131
Планарные графы стр. 154
-----------------------------------------------------------------
Уилсон Р. Введение в теорию графов. 1977
-----------------------------------------------------------------
Оре О. Теория графов. 1980
-----------------------------------------------------------------
Основной вывод таков:
Чем больше ребер будет при каждой вершине, тем больше там будет циклов. Число ребер должно превосходить число вершин.
Что касается пересечений, то тут больше сложностей. Граф без пересечений (на плоскости) или планарный граф можно нарисовать так, что ребра будут пересекаться. Придется перемещать вершины, чтобы убрать пересечения. Но предложенных книг достаточно, чтобы синтезировать требуемый алгоритм.
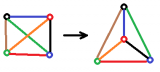
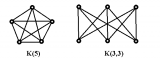
Тогда и только тогда неорграф G планарен, когда G не содержит подграфов, стягиваемых (т.е. получаемых последовательностью отождествлений вершин, связанных ребрами) к графу K(5) или K(3,3).
-----------------------------------------------------------------
Судоплатов С.В. Элементы дискретной математики. 2002
Элементы теории графов стр. 108
Маршруты. Достижимость. Связность стр. 119
Обходы графов стр. 131
Планарные графы стр. 154
-----------------------------------------------------------------
Уилсон Р. Введение в теорию графов. 1977
-----------------------------------------------------------------
Оре О. Теория графов. 1980
-----------------------------------------------------------------
Основной вывод таков:
Чем больше ребер будет при каждой вершине, тем больше там будет циклов. Число ребер должно превосходить число вершин.
Что касается пересечений, то тут больше сложностей. Граф без пересечений (на плоскости) или планарный граф можно нарисовать так, что ребра будут пересекаться. Придется перемещать вершины, чтобы убрать пересечения. Но предложенных книг достаточно, чтобы синтезировать требуемый алгоритм.

Тогда и только тогда неорграф G планарен, когда G не содержит подграфов, стягиваемых (т.е. получаемых последовательностью отождествлений вершин, связанных ребрами) к графу K(5) или K(3,3).

