Помогите решить задачу C++
Вычислить и вывести на печать с точностью 0.0001 значение суммы
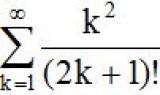
Попробывала так:
#include <stdio.h>
#include <math.h>
void main()
{
float a=1.,s=1.;
int k=1;
while (fabs(a)>0.0001)
{
a*=1./(2*k+1);
s+=a;
k++;
}
printf ("s=%f",s);
}
Но не уверена в правильности...
#include <iostream>
using namespace std;
#include <clocale>
#include <math.h>
int main()
{ int k=1;
double S, t;
float eps=0,0001;
setlocale (LC_CTYPE,"rus");
t=(pow( k,2)/(2*k+1));
S=t;
while (fabs(t)>eps)
{
k=k+1;
t=(pow( k,2)/(2*k+1));
S=S+t;
}
cout<<S<<" Вычисленно с заданной точностью "<<eps<<endl;
return 0 ;
}
Первое - считать каждый раз очередной член с нуля... Второе - считать с применением pow()... Третье - если считать, то не терять факториал, танкоградная программа просто не завершится :)
Четвертое - вообще-то для повышения точности суммы считаются обычно с меньшего члена к большему, ну да это простим :)
int main(int argc, const char * argv[])
{
double sum = 0.0;
double term = 1./6.;
for(int k = 1; term > 0.00001; ++k) // Точность - с запасом!
{
sum += term;
term *= (k+1)/(2.0*k*k*(2*k+3));
}
std::cout << sum << std::endl;
}
а то при вводе выявляются ошибки :(
Может, он cout не понимает? Замените
#include <iostream.h>
на
#include <stdio.h>
и
std::cout << sum << std::endl;
на
printf("Sum = %lf\n",sum);
Так работает?
И - если сообщаете об ошибках, не забывайте указывать - какие. Телепатов нет...
Убрала их из main и получился ответ 0.201786. У вас получился такой же ответ?
а можете это пояснить?
double sum = 0.0;
double term = 1./6.;
Это не ошибки, а предупреждения; программа должна компилироваться все равно....
Убрала их из main и получился ответ 0.201786. У вас получился такой же ответ?
Нет, это вы точность ухудшили... С моими параметрами (а не 0.0001) получается 0.20183. Дело в том, что все члены ряда - положительны, так что гарантировать, что сумма остатка меньше отброшенного члена нельзя (это для знакопеременных рядов). Потому я и брал точность ПОВЫШЕННУЮ.
double sum = 0.0;
double term = 1./6.;
Конечно, могу :) sum - здесь накапливаем сумму, term - текущий член, при k=1 равен 1/6. В цикле я для каждого k считаю член a_{k+1}...
Кстати, лучше переписать так (так самый последний член тоже будет добавлен, и для моего результата хватит даже точности 0.0001):
int main(int argc, const char * argv[])
{
double sum;
double term;
sum = term = 1./6.;
for(int k = 1; term > 0.00001; ++k) // Точность - с запасом!
{
term *= (k+1)/(2.0*k*k*(2*k+3));
sum += term;
}
std::cout << sum << std::endl;
}
void main(void)
{
long double summ,old,term,a,b;
int i = 1;
term = 1./6. ;
summ = term;
while(1)
{
printf("%.18Lf \n",summ);
i++;
a = i*i+2.*i+1;
b = 4.*i*i*i*i+10.*i*i*i+6.*i*i;
term = term*a/b;
old = summ;
summ = summ+term;
if((summ-old)==0.)break;
};
printf("%.18Lf",summ);
}
1*1/(2*1+1)! = 1/3! = 1/(1*2*3)=1/6
Где я ошибся?...
P.S. А вообще, глядя на ответы к этой задаче и встающие новые вопросы, все больше прихожу к решению - все, надо валить из этой темы, а то я и в самом деле начну сомневаться, действительно ли надо ли уметь думать, чтоб программировать... :(
1*1/(2*1+1)! = 1/3! = 1/(1*2*3)=1/6
Где я ошибся?...
P.S. А вообще, глядя на ответы к этой задаче и встающие новые вопросы, все больше прихожу к решению - все, надо валить из этой темы, а то я и в самом деле начну сомневаться, действительно ли надо ли уметь думать, чтоб программировать... :([/quote]
у мну тоже 1/6 . )
а вот итерационный множитель у вас неверен был .
и точность 0.00001 маловата для быстро сходящегося ряда .
а вот итерационный множитель у вас неверен был .
и точность 0.00001 маловата для быстро сходящегося ряда .
По второму вопросу - в задаче требуется 0.0001, я взял в 10 раз меньше. С учетом факториала для достижения точности 0.0001 вполне достаточно - убедитесь сами.
По первому... Знаете, давайте посчитаем руками для k=2:
2*2/(2*2+1)! =4/(1*2*3*4*5) = 1/30, т.е. 0.03333333...
Вставляем в мою программу вывод членов, и в вашу. Получаем
у меня - 0.03333...
у вас - 0.0089285714...
Так что не хочется вас обижать, но кто бы говорил :)
Еще по первому вопросу о точности. Вот промежуточные результаты:
Term = 0.0017857143, Sum = 0.2017857143
Term = 0.0000440917, Sum = 0.2018298060
Term = 0.0000006263, Sum = 0.2018304323
Term = 0.0000000058, Sum = 0.2018304381
О сравнительной эффективности наших программ молчу... Мои - 5 умножений, 1 деление, 3 сложения, у вас - 12 умножений, 5 сложений, 1 деление и 1 вычитание (кстати, я понимаю, что вы просто хотите использовать предел точности, но ведь проверка на равенство нулю при плавающей точке - большая некорректность даже в таком ее применении...).
Простите, ужасно не люблю, когда меня тычут носом в ошибки, которых у меня нет - тогда я зверею и тут уж под руку лучше не попадаться :)
double fact(int n)
{
double p = 1.0;
while(n > 1) p *= n--;
return p;
}
int main(int argc, const char * argv[])
{
double sum = 0;
double term = 1;
for(int k = 1; term > 0.00000001; ++k) // Точность - с запасом!
{
term = k*k/fact(2*k+1);
sum += term;
printf("Term = %.10lf, Sum = %.10lf\n",term,sum);
}
}
Term = 0.0333333333, Sum = 0.2000000000
Term = 0.0017857143, Sum = 0.2017857143
Term = 0.0000440917, Sum = 0.2018298060
Term = 0.0000006263, Sum = 0.2018304323
Term = 0.0000000058, Sum = 0.2018304381
a = i*i+2.*i+1;
b = 4.*i*i*i*i+10.*i*i*i+6.*i*i;
i++;
вот что значит на скорую руку писать )
с оптимизацией студень пусть сам справляется .
в каком месте сравнивать с нулём разность некорректно ?
summ = summ+term;
if((summ-old)==0.)break;
Ну и при таком решении точность-то все равно оказывается конкретно не оценена.
при таком решении точность определяется точностью типа данных .
при таком решении точность определяется точностью типа данных .
Вы ее можете конкретно назвать ДЛЯ РЕШЕНИЯ ЗАДАЧИ?
Т.е. ваш ответ - ........., с точностью ..........?
Так сказать, заполните пробелы... Реальные-то задачи решаются не для того, чтоб показать умение программировать, а чтобы решит математическую задачу... Понятно, что данная конкретная задача имеет конкретный ответ - (e^2-3)/(8*e), но представим, что ответ нам заранее неизвестен. Что вы можете сказать о точности своего ответа?
