Проверка временных пересечений многоугольников(полигонов)
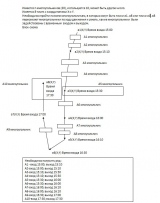
//проверка попадания точки в полигон
function IsPointInPolygon($xp, $yp, $x, $y)
{
$c = 0;
$npol = count($xp);
for ($i = 0, $j = $npol - 1; $i < $npol; $j = $i++)
{
if (((($yp[$i]<=$y) && ($y<$yp[$j])) || (($yp[$j]<=$y) && ($y<$yp[$i]))) &&
($x > ($xp[$j] - $xp[$i]) * ($y - $yp[$i]) / ($yp[$j] - $yp[$i]) + $xp[$i]))
$c = !$c;
}
return $c;
}
function square ($ax, $ay, $bx, $by, $cx,$cy) {
return $ax * ($by - $cy) + $bx * ($cy - $ay) + $cx * ($ay - $by);
}
function intersect_1 ($a, $b, $c, $d) {
return max_(a, b) >= min_(c, d) && max_(c, d) >= min_(a, b);
}
function intersect ($ax, $ay, $bx,$by, $cx,$cy, $dx,$dy) {
$s11 = square ($ax,$ay,$bx,$by,$cx,$cy);
$s12 = square ($ax,$ay,$bx,$by,$dx,$dy);
$s21 = square ($cx,$cy, $dx,$dy, $ax,$ay);
$s22 = square ($cx,$cy, $dx,$dy, $bx,$by);
if ($s11 == 0 && $s12 == 0 && $s21 == 0 && $s22 == 0)
return intersect_1 ($ax, $bx, $cx, $dx)
&& intersect_1 ($ay, $by, $cy, $dy);
else
return ($s11 * $s12 <= 0) && ($s21 * $s22 <= 0);
}
//проверка пересечения линии с полигоном
function IsCrossLineWithPolygon($xp, $yp, $x1, $y1,$x2,$y2)
{
$c= 0;
$npol = count($xp); $j = 0;
for ($i = 0; $i < $npol; $i++)
{
if ($i != ($npol-1))
$j = $i+1;
else
$j = 0;
if (intersect($xp[$i],$yp[$i],$xp[$j],$yp[$j],$y1,$x1,$y2,$x2))
return 1;
}
return 0;
}
function IsInPoly($pointArX, $pointArY, $oldx, $oldy,$curx,$cury)
{
if (IsCrossLineWithPolygon($pointArX, $pointArY, $oldx, $oldy,$curx,$cury)
|| IsPointInPolygon($pointArY, $pointArX,$curx,$cury) )
{
return true;
}
return false;
}
Не могу сформировать алгоритм в общем виде
$oldx = 0; $oldy = 0;
$x = 0; $y = 0;
$dat = "";
//проверка по массиву точек
for ($i =0; $i < count($a); $i++)
{
$oldx = $x; $oldy= $y;
$x = $a[$i].X; $y = $a[$i].Y;
$dat = $a[$i].Data;
//поиск по массиву многоугольников
for ($t=0; $t < count($A); $t++)
{
//если точка находится в полигоне или его пересекает
if ( IsInPoly($A,$oldx,$oldy,$x,$y))
{
printf("Точка входа в полигон %s в %s",$A[$t],$dat);
}
//а дальше не понятно, как сохранять и использовать входы и выходы?
}
}
Есть ли у кого-нибудь оптимальный материал или алгоритм?
Спасибо.
Решение найдено, очень долго пришлось самому создавать код.
