Как строить граф достижимости сети Петри?
Народ, помогите разобраться с построением графа достижимости сети Петри.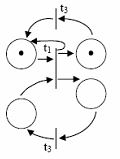

Проименуйте позиции (места) сети Петри.
Зафиксировать начальную маркировку. На рисунке у вас M0={1,1,0,0}, если именовать места слева на право, сверху вниз: s1, s2, s3 и s4.
M0 - это начальная (корневая) вершина дерева, с которой начинаем построение.
Далее в цикле обычные действия: взять список возбужденных переходов в текущей вершине, сработать каждый переход, получить новую маркировка - новую вершину дерева. Если получили маркировка, которая уже была в дереве, рисуем дугу на нее, а новую вершину удаляем. Есть еще символ омега для бесконечных маркировок. Проверяем, если новая маркировка строго больше текущей для данной позиции сети, значит происходит накопление и тогда объявляем маркировку вершины дерева как, например {w,0,1,1}.
Для вашего рисунка:
0: M={1,1,0,0} : может сработать только t3 => M'={2,0,0,0} -> 1:
1: M={1,0,0,0} : больше не может сработать ни один переход. Конец построения.
Зафиксировать начальную маркировку. На рисунке у вас M0={1,1,0,0}, если именовать места слева на право, сверху вниз: s1, s2, s3 и s4.
M0 - это начальная (корневая) вершина дерева, с которой начинаем построение.
Далее в цикле обычные действия: взять список возбужденных переходов в текущей вершине, сработать каждый переход, получить новую маркировка - новую вершину дерева. Если получили маркировка, которая уже была в дереве, рисуем дугу на нее, а новую вершину удаляем. Есть еще символ омега для бесконечных маркировок. Проверяем, если новая маркировка строго больше текущей для данной позиции сети, значит происходит накопление и тогда объявляем маркировку вершины дерева как, например {w,0,1,1}.
Для вашего рисунка:
0: M={1,1,0,0} : может сработать только t3 => M'={2,0,0,0} -> 1:
1: M={1,0,0,0} : больше не может сработать ни один переход. Конец построения.
