Метод Эйлера для сложного дифура, или что не так с моей математикой?
Доброго времени суток! Итак, довольно тривиальное задание в университете поставило меня в окончательный тупик. В общих чертах задача - решить диф. ур. второго порядка методом Эйлера. Я себе это представил следующим образом:
Полностью задание есть в прикрепленном pdf.
Беда в том, что числа очень быстро уходят в бесконечность. Укажите, пожалуйста, на мою ошибку.
Код:
#include "stdafx.h"
#include <math.h>
#include <stdio.h>
#define M_PI 3.1415926535897932384626433832795
double h = 0.0001;
FILE *myfile;
const double H=0.25;
const double ro = 500;
const double angle =1.05/2; //60 grdusov v radianah
const double roLiq = 1000;
const double resist = 150; //f
const double x0 = 0.5;
const double v0 = 0;
const double t0=0;
const double tmax=3;
const double deltat = h;
const double g = 9.81;
double m;
double h0;
FILE *result;
void init()
{
m= ((M_PI*ro)/3.)*pow(tan(angle),2)*pow(H,3);
h0=H*pow(ro/roLiq,1./3.);
result = fopen("result.txt","w");
}
//y=dx
//z=dy
double z (double y)
{
return y;
}
double dz (double x, double z)
{
double p1=((M_PI*pow(tan(angle),2)*pow(h0-x,2))/m);
double p2=((roLiq*g)/3)*(h0-x);
double p3=((resist/sin(angle))*z);
double dz =-g+(((M_PI*pow(tan(angle),2)*pow(h0-x,2))/m)*(((roLiq*g)/3.)*(h0-x)-(resist/sin(angle))*z));
//double dz=-g+(3270/(h0-x)-30*z)*pow(h0-x,2);
return dz;
}
void solve()
{
double xc = x0;
double yc=v0;
double zc = 0;
double c=0;
for(double i=t0;i<tmax;i+=deltat)
{
c++;
double xc1 = xc+yc*h;
double yc1=yc+h*zc;
double zc1 = zc+h*dz(xc,yc);
/*double k1 = dz(xc,yc);
double k2=dz(xc+h/2,yc+h/2*k1);
double k3 = dz(xc+h/2,yc+h/2*k2);
double k4 = dz(xc+h,yc+h*k3);
double zc1 = zc+h/6*(k1+2*k2+2*k3+k4);
*/
fprintf(result,"%ft%ft%ft%fn",i,xc-h0,yc,zc);
xc=xc1;
yc=yc1;
zc=zc1;
}
}
int _tmain(int argc, _TCHAR* argv[])
{
init();
solve();
fclose(result);
return 0;
}
#include <math.h>
#include <stdio.h>
#define M_PI 3.1415926535897932384626433832795
double h = 0.0001;
FILE *myfile;
const double H=0.25;
const double ro = 500;
const double angle =1.05/2; //60 grdusov v radianah
const double roLiq = 1000;
const double resist = 150; //f
const double x0 = 0.5;
const double v0 = 0;
const double t0=0;
const double tmax=3;
const double deltat = h;
const double g = 9.81;
double m;
double h0;
FILE *result;
void init()
{
m= ((M_PI*ro)/3.)*pow(tan(angle),2)*pow(H,3);
h0=H*pow(ro/roLiq,1./3.);
result = fopen("result.txt","w");
}
//y=dx
//z=dy
double z (double y)
{
return y;
}
double dz (double x, double z)
{
double p1=((M_PI*pow(tan(angle),2)*pow(h0-x,2))/m);
double p2=((roLiq*g)/3)*(h0-x);
double p3=((resist/sin(angle))*z);
double dz =-g+(((M_PI*pow(tan(angle),2)*pow(h0-x,2))/m)*(((roLiq*g)/3.)*(h0-x)-(resist/sin(angle))*z));
//double dz=-g+(3270/(h0-x)-30*z)*pow(h0-x,2);
return dz;
}
void solve()
{
double xc = x0;
double yc=v0;
double zc = 0;
double c=0;
for(double i=t0;i<tmax;i+=deltat)
{
c++;
double xc1 = xc+yc*h;
double yc1=yc+h*zc;
double zc1 = zc+h*dz(xc,yc);
/*double k1 = dz(xc,yc);
double k2=dz(xc+h/2,yc+h/2*k1);
double k3 = dz(xc+h/2,yc+h/2*k2);
double k4 = dz(xc+h,yc+h*k3);
double zc1 = zc+h/6*(k1+2*k2+2*k3+k4);
*/
fprintf(result,"%ft%ft%ft%fn",i,xc-h0,yc,zc);
xc=xc1;
yc=yc1;
zc=zc1;
}
}
int _tmain(int argc, _TCHAR* argv[])
{
init();
solve();
fclose(result);
return 0;
}
Беда в том, что числа очень быстро уходят в бесконечность. Укажите, пожалуйста, на мою ошибку.
Написал свой вариант Вашей программы с комментариями.
Причина ухода значений в бесконечность состоит в слишком большом шаге интегрирования, но более вероятны ошибки в написанной Вами программе, их много. В этой задаче шаг не должен быть больше 0,001 секунды. Для метода Эйлера это обычное поведение, поэтому лучше использовать неявный метод Эйлера переменного шага.
Вот результат при шаге 0,0005.
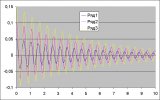
Перед применением метода Эйлера следует некоторым образом преобразовать исходное уравнение:

Причина ухода значений в бесконечность состоит в слишком большом шаге интегрирования, но более вероятны ошибки в написанной Вами программе, их много. В этой задаче шаг не должен быть больше 0,001 секунды. Для метода Эйлера это обычное поведение, поэтому лучше использовать неявный метод Эйлера переменного шага.
Вот результат при шаге 0,0005.

Перед применением метода Эйлера следует некоторым образом преобразовать исходное уравнение:

Код:
// Проверено в Dev-C++ 4.9.9.2
#include <cstdlib>
#include <iostream>
#include <math.h>
#include <fstream>
#include <iomanip>
using namespace std;
//------------------------------------------
// ВАЖНО! Чем меньше глобальных переменных -
// тем лучше, но так как это тестовый учебный
// пример, который нужен, чтобы понять принцип,
// то можно закрыть на это глаза.
// ВАЖНО! Крайне опасны однобуквенные глобальные
// переменные.
//------------------------------------------
const int Nv = 2,//число переменных (уравнений)
Nt = 3;//число различных начальных условий
//------------------------------------------
// Параметры модели
//------------------------------------------
double g = 9.80665, //ускорение силы тяжести, м/(с*с)
H = 0.25, //высота конуса, м
rho = 500.0, //плотность материала конуса, кг/(м*м*м)
rholiq = 1000.0, //плотность жидкости, кг/(м*м*м)
alpha = 0.5*60.0,//угол полу-раствора конуса, градусов
f = 15.0, //коэффициент сопротивления, Н*с/(м*м*м)
v0 = 0.0, //начальная скорость тела, м/с
t0 = 0.0, //начальное время моделирования, с
tmax = 10.0, //конечное время моделирования, с
x0[Nt] = {0.05,
0.1,
0.15};//три варианта начальных смещений конуса, м
double alphar = M_PI*alpha/180.0;//угол полу-раствора конуса, радиан
double h0 = H*pow((rho/rholiq),(1.0/3.0)),//глубина погружения в положении равновесия
m = M_PI*rho*H*H*H*tan(alphar)*tan(alphar)/3.0;//масса конуса
double c = M_PI*tan(alphar)*tan(alphar)/m,
d = rholiq*g/3.0,
e = f/sin(alphar);
//------------------------------------------
// Параметры численного метода
//------------------------------------------
// Желательно, чтобы шаг по времени мог быть
// представлен степенью двойки, а именно
// в форме N/(2^Z). Где N - натуральное, а
// Z - целое число. Например, 1.0/(2.0*2.0*...*2.0).
// 0.125 0.0625
double dt = 1.0/(2.0*2.0*2.0*2.0*2.0*2.0*2.0*2.0*2.0*2.0*2.0),//шаг по времени, с
time_c = 0.0,//текущее время
X[Nv],//переменные
F[Nv];//производные
int points = (int)((tmax - t0)/dt) + 1;
double **result;
//------------------------------------------
// Достаточно распространенная форма представления
// систем уравнений при решении численными методами
//------------------------------------------
void SystemODE(double t,double *X,double *F){
// t - время (в данную систаму ОДУ не входит)
// F[0] - dx/dt, X[0] - x
// F[1] - dy/dt, X[1] - y
// g = g модели
// c = pi*tg(alpha)*tg(alpha)/m
// d = rho(liq)*g/3
// e = f/sin(alpha)
F[0] = X[1];// dx/dt = y
F[1] = -g + c*(h0-X[0])*(h0-X[0]) * (d*(h0-X[0]) - e*X[1]);// dy/dt = F(x,y)
}
//------------------------------------------
void EulerStep(double t,double *X,double *F){
SystemODE(t,X,F);
for(int i=0;i<Nv;i++)
X[i] = X[i] + dt * F[i];
}
//------------------------------------------
void Calc(void){
//Массив для хранения и печати результатов
result = new double * [points];
for(int j=0;j<points;j++)
result[j] = new double [Nt+1];
//Цикл по вариантам расчета
for(int i=0;i<Nt;i++){
//Начальные условия
time_c = t0;
X[0] = x0[i];
X[1] = v0;
//Цикл по расчетным точкам
for(int j=0;j<points;j++){
result[j][0] = time_c;
result[j][i+1] = X[0];
EulerStep(time_c,X,F);
time_c += dt;
}
}
//Печать результата
fstream fs;
fs.open("result.txt",std::fstream::out | std::fstream::trunc);
int digit = 5;
//fs << std::scientific;
fs << std::fixed;
fs << std::setprecision(digit);
//cout << std::scientific;
cout << std::fixed;
cout << std::setprecision(digit);
for(int j=0;j<points;j++){
for(int i=0;i<=Nt;i++){
cout << result[j][i] << "t";
fs << result[j][i] << "t";
}
cout << "n";
fs << "n";
}
fs.close();
//Удаление массива результатов
for(int j=0;j<points;j++){
delete [] result[j];
result[j] = NULL;
}
delete [] result;
result = NULL;
}
//------------------------------------------
int main(int argc, char *argv[]){
Calc();
system("PAUSE");
return EXIT_SUCCESS;
}
//------------------------------------------
#include <cstdlib>
#include <iostream>
#include <math.h>
#include <fstream>
#include <iomanip>
using namespace std;
//------------------------------------------
// ВАЖНО! Чем меньше глобальных переменных -
// тем лучше, но так как это тестовый учебный
// пример, который нужен, чтобы понять принцип,
// то можно закрыть на это глаза.
// ВАЖНО! Крайне опасны однобуквенные глобальные
// переменные.
//------------------------------------------
const int Nv = 2,//число переменных (уравнений)
Nt = 3;//число различных начальных условий
//------------------------------------------
// Параметры модели
//------------------------------------------
double g = 9.80665, //ускорение силы тяжести, м/(с*с)
H = 0.25, //высота конуса, м
rho = 500.0, //плотность материала конуса, кг/(м*м*м)
rholiq = 1000.0, //плотность жидкости, кг/(м*м*м)
alpha = 0.5*60.0,//угол полу-раствора конуса, градусов
f = 15.0, //коэффициент сопротивления, Н*с/(м*м*м)
v0 = 0.0, //начальная скорость тела, м/с
t0 = 0.0, //начальное время моделирования, с
tmax = 10.0, //конечное время моделирования, с
x0[Nt] = {0.05,
0.1,
0.15};//три варианта начальных смещений конуса, м
double alphar = M_PI*alpha/180.0;//угол полу-раствора конуса, радиан
double h0 = H*pow((rho/rholiq),(1.0/3.0)),//глубина погружения в положении равновесия
m = M_PI*rho*H*H*H*tan(alphar)*tan(alphar)/3.0;//масса конуса
double c = M_PI*tan(alphar)*tan(alphar)/m,
d = rholiq*g/3.0,
e = f/sin(alphar);
//------------------------------------------
// Параметры численного метода
//------------------------------------------
// Желательно, чтобы шаг по времени мог быть
// представлен степенью двойки, а именно
// в форме N/(2^Z). Где N - натуральное, а
// Z - целое число. Например, 1.0/(2.0*2.0*...*2.0).
// 0.125 0.0625
double dt = 1.0/(2.0*2.0*2.0*2.0*2.0*2.0*2.0*2.0*2.0*2.0*2.0),//шаг по времени, с
time_c = 0.0,//текущее время
X[Nv],//переменные
F[Nv];//производные
int points = (int)((tmax - t0)/dt) + 1;
double **result;
//------------------------------------------
// Достаточно распространенная форма представления
// систем уравнений при решении численными методами
//------------------------------------------
void SystemODE(double t,double *X,double *F){
// t - время (в данную систаму ОДУ не входит)
// F[0] - dx/dt, X[0] - x
// F[1] - dy/dt, X[1] - y
// g = g модели
// c = pi*tg(alpha)*tg(alpha)/m
// d = rho(liq)*g/3
// e = f/sin(alpha)
F[0] = X[1];// dx/dt = y
F[1] = -g + c*(h0-X[0])*(h0-X[0]) * (d*(h0-X[0]) - e*X[1]);// dy/dt = F(x,y)
}
//------------------------------------------
void EulerStep(double t,double *X,double *F){
SystemODE(t,X,F);
for(int i=0;i<Nv;i++)
X[i] = X[i] + dt * F[i];
}
//------------------------------------------
void Calc(void){
//Массив для хранения и печати результатов
result = new double * [points];
for(int j=0;j<points;j++)
result[j] = new double [Nt+1];
//Цикл по вариантам расчета
for(int i=0;i<Nt;i++){
//Начальные условия
time_c = t0;
X[0] = x0[i];
X[1] = v0;
//Цикл по расчетным точкам
for(int j=0;j<points;j++){
result[j][0] = time_c;
result[j][i+1] = X[0];
EulerStep(time_c,X,F);
time_c += dt;
}
}
//Печать результата
fstream fs;
fs.open("result.txt",std::fstream::out | std::fstream::trunc);
int digit = 5;
//fs << std::scientific;
fs << std::fixed;
fs << std::setprecision(digit);
//cout << std::scientific;
cout << std::fixed;
cout << std::setprecision(digit);
for(int j=0;j<points;j++){
for(int i=0;i<=Nt;i++){
cout << result[j][i] << "t";
fs << result[j][i] << "t";
}
cout << "n";
fs << "n";
}
fs.close();
//Удаление массива результатов
for(int j=0;j<points;j++){
delete [] result[j];
result[j] = NULL;
}
delete [] result;
result = NULL;
}
//------------------------------------------
int main(int argc, char *argv[]){
Calc();
system("PAUSE");
return EXIT_SUCCESS;
}
//------------------------------------------
поясните в что вы имеете ввиду под словом бесконечность
Цитата: cronya
поясните в что вы имеете ввиду под словом бесконечность
уходят далеко за пределы MAX_DOUBLE. И вообще, колебательный процесс должен быть затухающим, а у меня как раз наоборот.
